Robinson called this the orthophanic projection (which means “right appearing”), but this name never caught on. In at least one reference book, this projection is termed the Pseudocylindrical Projection with Pole Line, which is highly descriptive (the “pole line” comes from the fact that the North and South Poles on a Robinson projection are shown as lines and not points), but so unwieldily that it is not surprising that this name also failed to gain much acceptance.
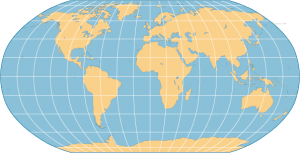
The “Robinson projection” is unquestionably the name of choice. The Robinson projection is highly unique. Unlike all other projections, Professor Robinson did not develop this projection by developing new geometric formulas to convert latitude and longitude coordinates from the surface of the Model of the Earth to locations on the map. Instead, Robinson used a huge number of trial-and-error computer simulations to develop a table that allows a cartographer to look up how far above or below a Robinson map’s equator a particular line of latitude will be located, and then to estimate (via a simple interpolation process) where along this line a particular longitude will fall. To this day, no other projection uses this approach to build a map.
Form:
The Robinson projection can best be described as being pseudocylindrical, but given its unique method of development, it does not fall perfectly into any known form category.
Case:
The Robinson projection is basically secant, with lines of tangency running along the 38° 0′ 0″N and 38° 0′ 0″S lines of latitude.
Aspect:
Robinson projections have normal aspects.
Variation Within Robinson Projections:
Robinson projections differ from one another in the locations of their central meridians.
Distortions
Shearing:
The Robinson projection is not conformal; shapes are distorted more than they would be in a truly conformal projection. However, shapes are not distorted very badly within about 45° north or south of the equator or within about 45° of the map’s central meridian. Beyond these limits, shape distortion can be quite severe.
Tearing:
Robinson maps show lines of latitude as parallel straight lines and lines of longitude as nonparallel lines that become increasingly curved as you move farther away from the map’s central meridian. The poles are shown as straight lines (0.5322 times as long as the equator) and the east and west edges of the map are curved lines 180° from the map’s central meridian. These east and west edges are markedly less curved than are the edges of other pseudocylindrical projections (the result being that the Robinson projection generally suffers from less shearing than do other pseudocylindrical projections). Tearing occurs along the edges of a Robinson map.
Compression:
Robinson projections are not equivalent; they do suffer from compression. However, the amount of area distortion is generally low within about 45° of the equator.
Equivalence:
Robinson projections are not equivalent; they do suffer from compression. However, the amount of area distortion is generally low within about 45° of the equator.
Conformality:
The Robinson projection is not conformal; shapes are distorted more than they would be in a truly conformal projection. However, shapes are not distorted very badly within about 45° north or south of the equator or within about 45° of the map’s central meridian.
Equidistance:
The Robinson projection is not equidistant; there is no point or points from which all distances are shown accurately.
Azimuthality:
The Robinson projection is not azimuthal; there is no point or points from which all directions are shown accurately.
Uses
The Robinson projection is unique. Its primary purpose is to create visually appealing maps of the entire world. It is a compromise projection; it does not eliminate any type of distortion, but it keeps the levels of all types of distortion relatively low over most of the map.
Source:
-Denis J. Dean, Colorado State University
